Zi-wei Lin Discusses a Multiphase Transport Model for Relativistic Heavy Ion Collisions
Special Topic of Hadron Colliders Interview, June 2011

|
The paper "Multiphase transport model for relativistic heavy ion collisions," (Lin ZW, et al.,Phys. Rev. C 72[6]: art. no. 064901, December 2005) is a key paper in the Research Front Map on Hadron Colliders, with 116 cites at the time the Special Topics analysis was run. Currently in Essential Science IndicatorsSM from Thomson Reuters, it is also a Highly Cited Paper in the field of Physics, with 133 citations up to February 28, 2011. The paper's lead author is Dr. Zi-Wei Lin, who is Assistant Professor in Physics at East Carolina University in Greenville, North Carolina. |
In this interview, Lin talks with ScienceWatch.com about this paper and its impact on the field of hadron colliders.
![]() Why do you think your paper is highly
cited?
Why do you think your paper is highly
cited?
The first reason is that the paper provides a comprehensive description of a multi-phase transport (AMPT) model, which includes the most complete treatment of different physical stages at the time for the simulation of the collisions of two high-energy ions. The second reason that makes the paper and the transport model popular is that the transport model implements a full parton phase followed by a quark coalescence model that describes the transition of a quark and anti-quark matter to a hadron matter.
We put the source code of this Monte Carlo transport model online in 2004. Since then many physicists and a number of heavy ion experimental collaborations have used the transport model to simulate nuclear collisions, compare with experimental data, and study possible new observables of the dense matter created in these collisions.
![]() Does it describe a new discovery,
methodology, or synthesis of knowledge?
Does it describe a new discovery,
methodology, or synthesis of knowledge?
Our transport model, which this paper describes in detail, combines for the first time the multiple phases that the matter created in a high-energy nuclear collision is expected to go through. The model includes the initial parton productions from the two colliding nuclei, the parton phase where quarks, anti-quarks, and gluons interact, the transition from partons to hadrons, and the subsequent hadron interaction phase. Therefore this transport model can be used as a versatile tool to study parton interactions and hadron interactions simultaneously and to study the evolution and properties of the dense matter in general.
![]() Would you summarize the significance of your
paper in layman's terms?
Would you summarize the significance of your
paper in layman's terms?
Figure 1:
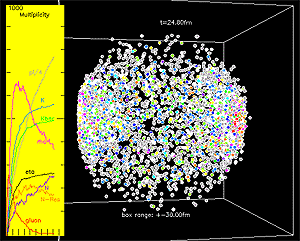
"...a single collision of two high-energy gold nuclei
using the simulation data from a version of this transport
model..."
View larger ANIMATED FIGURE & FULL DESCRIPTION in
tab below.
The Monte Carlo transport model described by the paper provides the ability to simulate high-energy nuclear collisions from start to finish. The attached animation shows the time-evolution of a single collision of two high-energy gold nuclei using the simulation data from a version of this transport model. The two nuclei come from the left and right side respectively. Here time t in the center-of-mass frame starts from the instant when the two nuclei overlap and stops at 30 femtometers over the speed of light, i.e., 10-22 second, and the box is 60 femtometers long along each axis. Partons such as gluons (in red) are produced first and then interact with each other. Then hadrons appear and partons gradually convert to hadrons, and the dense matter expands fast and reaches lower densities. Hadrons, such as pions (in gray), kaons (in blue), and anti-kaons (in green), interact with each other and are sometimes destroyed or reproduced, and resonances such as rho mesons (in magenta) also gradually decay. The total numbers or multiplicities of different particle types at different times are shown in the left panel of the animation. The evolution of the matter at the far right or the far left side has a strong time dilation due to Einstein’s theory of special relativity, so gluons can still be seen there at the end of this animation where essentially all the gluons in the middle have already been converted to hadrons.
Because a high-energy nuclear collision is a complicated process that involves the creation of the quark-gluon plasma, a dense matter that consists of interacting quarks, anti-quarks, and gluons, there is plenty of physics that we can explore. A lot of the physical processes that we understand poorly are being represented by parameters in the transport model; therefore physicists can study the possible effects of the unknown physics by varying those parameters within an estimated range.
In the meantime, physicists can compare the simulated data from the model with the actual experimental data from different facilities, including the Relativistic Heavy Ion Collider (RHIC) in the US and the Large Hadron Collider (LHC) in Europe. These comparisons help physicists to better understand the meaning of the experimental data and distinguish the interesting effects of the unknown physics from the complicated effects of the known physical processes.
![]() How did you become involved in this research,
and how would you describe the particular challenges, setbacks, and
successes that you've encountered along the way?
How did you become involved in this research,
and how would you describe the particular challenges, setbacks, and
successes that you've encountered along the way?
I started working in the area of Monte Carlo transport models when I went to Texas A&M University in 1998 as a research associate in Dr. Ko’s group. All the authors of this paper have spent time in this group on the development and applications of Monte Carlo transport models for nuclear reactions.
Our first goal was to build a transport model for high-energy nuclear collisions that contains both the parton phase and the hadron phase. At that time, there were already event generators and Monte Carlo cascade models available for the initial parton productions, parton interactions, and hadron interactions, but they were separate models that only contained one of these components. We took advantage of the existing models by attempting to combine them consistently.
Our first challenge was to find self-consistent ways to connect these multiple phases, for example, to provide space-time information for the initial partons so that they can interact with each other in the parton cascade phase, and to convert all the partons into hadrons after the partons have completed their interactions.
Our first construction of a multi-phase transport model was completed in time so that we were able to provide predictions to the "RHIC Theory Competition" for the collisions of two gold nuclei before the collisions took place in 2000 at the Brookhaven National Laboratory. Two years later, the winners of that competition were selected at a workshop held at the Institute for Nuclear Theory, and our model was selected as the best overall transport model for RHIC predictions. What made the event even more unforgettable is that the winning competitors each received a bottle of excellent Washington State wine bought by the organizers when they announced the competition in 1998.
"The Monte Carlo transport model described by the paper provides the ability to simulate high-energy nuclear collisions from start to finish."
We then further developed the AMPT model and compared the predicted results with the excellent RHIC data on multiple observables. Soon we realized that our transport model produced too-small elliptic flows; actually almost all transport models at that time gave too weak elliptic flows. The elliptic flow observables represent how asymmetric the final particles are in the plane transverse to the beam direction and they have played very important roles in heavy-ion physics. This is because they can tell us how strongly the early dense matter interacts; it was later realized that they may also give us key information about how partons organized themselves into hadrons through quark coalescence or parton recombination.
This presented another challenge for us, which prompted us to introduce the idea of string melting in the multi-phase transport model. As a result, we were able to show that, by melting the wounded nucleons from the two overlapping nuclei in the collision into partons, the subsequent parton interactions followed by hadron interactions can produce elliptic flow signals as big as in the RHIC data.
![]() Where do you see your research leading in the
future?
Where do you see your research leading in the
future?
A multi-phase transport model simulates the expected full evolution of the matter created in a high-energy nuclear collision, but it is especially challenging to incorporate the equation of state of the QCD phase transition in a transport model. Therefore it is often difficult to infer certain properties of the dense matter using a transport model. In the past few years we have only made incremental improvements and provided user support for the multi-phase transport model.
On the other hand, Monte Carlo transport models such as our model can provide important advantages for the study of the dynamics of the dense matter produced in nuclear collisions. For example, they can offer rich insight into the microscopic processes driving the non-equilibrium evolution of a heavy ion collision, and they also directly address the parton and hadron degrees of freedom in the dynamical parton recombination process.
As for all approaches that investigate the fascinating matter created in heavy ion collisions, there are conceptual as well as technical challenges for the Monte Carlo transport model approach. For example, if the dense matter turns out to be so strongly coupled in the early stage that one should abandon the quasi-particle picture, the early time dynamics would need to be described by another model, and the transport model would be used after this strong-coupling stage.
In the near future we would like to use the transport model as a tool to study whether parton recombination is a good description of the bulk hadronization process through which partons change to hadrons. We also plan to further develop the Monte Carlo transport model to better study the properties of the dense QCD matter, especially for heavy-ion collisions at the new LHC.
![]() Do you foresee any social or political
implications for your research?
Do you foresee any social or political
implications for your research?
Understanding the evolution and properties of the dense matter created in
high-energy nuclear collisions is closely related to understanding the very
early universe, because we believe that the universe at about a microsecond
after the Big Bang went through similar energy densities and a similar
phase transition. Our research helps satisfy our desire to understand
nature but may not have foreseeable social or political
implications.![]()
Zi-Wei Lin, Ph.D.
Assistant Professor
Department of Physics
East Carolina University
Greenville, NC, USA
ZI-WEI LIN'S MOST CURRENT MOST-CITED PAPER IN ESSENTIAL SCIENCE INDICATORS:
Lin ZW, et al., "Multiphase transport model for relativistic heavy ion collisions," Phys. Rev. C 72(6): art. no. 064901, December 2005 with 133 cites. Source: Essential Science Indicators from Clarivate .
KEYWORDS: MULTIPHASE TRANSPORT MODEL, RELATIVISTIC HEAVY ION COLLISIONS, FULL PARTON PHASE, QUARK COALESCENCE MODEL, MONTE CARLO TRANSPORT MODEL, QUARK, ANTI-QUARK, HADRON, HIGH-ENERGY NUCLEAR COLLISIONS, DENSE MATTER, MULTIPLE PHASES, PARTON INTERACTIONS, HADRON INTERACTIONS, GOLD, PIONS, KAONS, ANTI-KAONS, RHO MESONS, TIME DILATION, EINSTEIN’S THEORY OF SPECIAL RELATIVITY, GLUONS, QUARK-GLUON PLASMA, SIMULATED DATA, EXPERIMENTAL DATA, RHIC PREDICTIONS, ELLIPTIC FLOW, BIG BANG.
Figure 1:
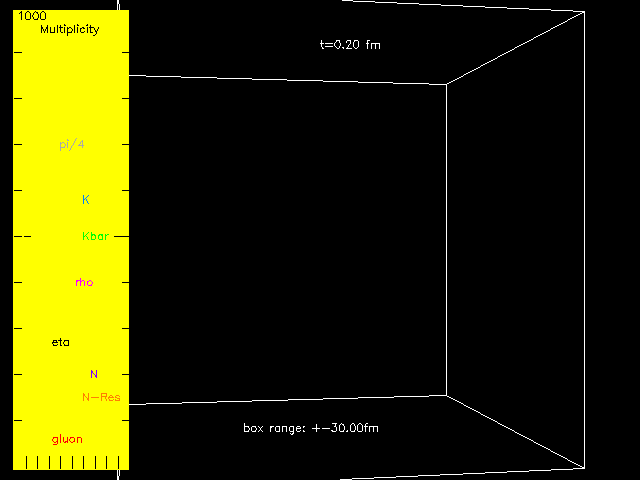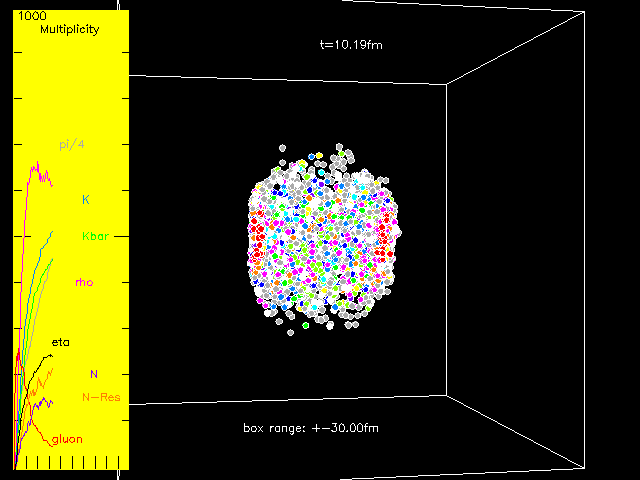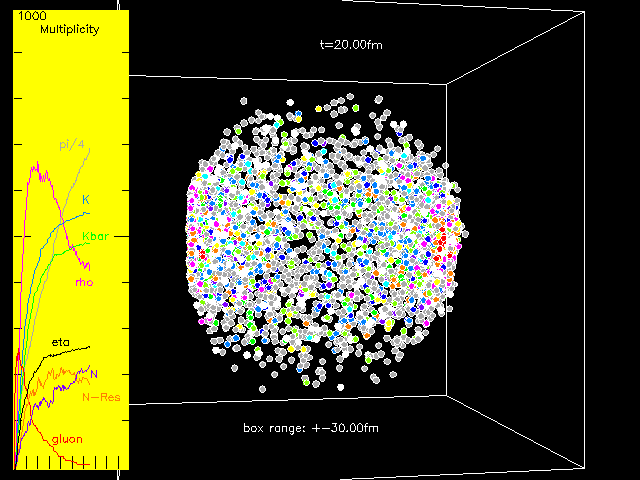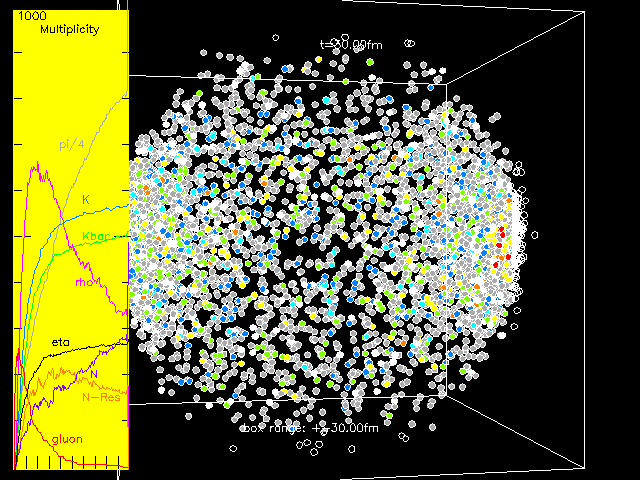
Figure 1:
The animation of a single collision of two high-energy gold nuclei using the simulation data from a version of this transport model. The two nuclei come from the left and right side respectively. Here time t in the center-of-mass frame starts from the instant when the two nuclei overlap and stops at 30 femtometers over the speed of light, i.e., 10-22 second, and the box is 60 femtometers long along each axis. Partons such as gluons (in red color) are produced first and then interact with each other. Then hadrons appear and partons gradually convert to hadrons, and the dense matter expands fast and reaches lower densities. Hadrons, such as pions (in gray), kaons (in blue), and anti-kaons (in green), interact with each other and are sometimes destroyed or reproduced, and resonances such as rho mesons (in magenta) also gradually decay. The total numbers or multiplicities of different particle types at different times are shown in the left panel of the image. The evolution of the matter at the far right or the far left side has a strong time dilation due to Einstein’s theory of special relativity, so gluons can still be seen there at the end of this animation where all the gluons in the middle have already converted to hadrons.
