Martin Ostoja-Starzewski Talks About Material Spatial Randomness
Emerging Research Front Commentary, December 2010

|
Article: Material spatial randomness: From statistical to representative volume element
Authors: Ostoja-Starzewski, M 2006 PROBABILISTIC ENG MECH paper, "Material spatial randomness: From statistical to representative volume element |
Martin Ostoja-Starzewski talks with ScienceWatch.com and answers a few questions about this month's Emerging Research Front paper in the field of Engineering.
![]() Why do you think your paper is highly
cited?
Why do you think your paper is highly
cited?
For several decades now scientists have been grappling with problems at the intersection of mechanics of materials, random media, and scaling issues. This paper collected a number of results and synthesized them into a new approach. In effect, it defined a new methodology of handling such problems, using a combination of analytical mechanics, probability theory, image analysis, and computational methods.
Does it describe a new discovery, methodology, or synthesis of knowledge?
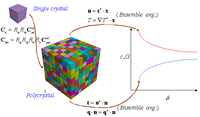
The key obstacle to using conventional solid mechanics in random media problems is the lack of validity of the so-called Representative Volume Element (RVE). The RVE used to be taken for granted in many stochastic solid mechanics studies, yet that was in stark contrast with basic physical considerations related to scale dependence, Fig. 1.
In other words, the separation of scales does not generally hold in random media problems, which led me to propose a so-called Statistical Volume Element (SVE), allowing a researcher to qualitatively and quantitatively predict the passage of constitutive responses from the SVE to the RVE as the scale increases.
Would you summarize the significance of your paper in layman's terms?
Homogenization methodology for second- and fourth-rank
tensors.
VIEW/Download additional figures and descriptions of
Martin Ostoja-Starzewski's work.
The aforementioned SVE is the material domain over which homogenization is being carried out—it is called the mesoscale, separating the microscale (level of microheterogeneities) from the macroscale (level of RVE). As the mesoscale grows, the SVE tends to become the RVE. This occurs in terms of two hierarchies of bounds stemming from the so-called Dirichlet and Neumann boundary value problems on the mesoscale, respectively, Fig. 2. Those bounds follow from the extremum principles of mechanics.
Since generally there is no periodicity in real random media, the RVE can only be approached approximately on finite scales, and this approach may be either rapid, moderate or slow—this can be assessed. The methodology can handle a very wide range of constitutive responses in various materials (e.g. composites, metals, porous media): linear elasticity, finite elasticity, plasticity, viscoelasticity, thermoelasticity, permeability of partially/fully saturated media, linear and nonlinear conductivity (thermal, electrical, etc.), as well as multifield problems in thermomechanics and material-electromagnetic interactions.
How did you become involved in this research, and how would you describe the particular challenges, setbacks, and successes that you've encountered along the way?
I've been involved in various aspects of stochastic solid mechanics most of my research career. Besides conceptual and theoretical difficulties, the challenge was to introduce the new way of thinking (as described in this article) to the scientific community, because it presented a new viewpoint of initial-boundary value problems involving material spatial randomness.
These problems are qualitatively different from random vibration problems, i.e. vibration of structural elements—rods, plates, shells, which are deterministic in their spatial structure—under random forcing. Thus, different stochastic and computational methods had to be introduced instead of directly adapting those from the latter field. This work is still evolving.
Where do you see your research leading in the future?
"The key obstacle to using conventional solid mechanics in random media problems is the lack of validity of the so-called Representative Volume Element (RVE)"
This research (and, in fact, this paper) has led to a book, Microstructural Randomness and Scaling in Mechanics of Materials (2008), new graduate courses, invited seminars, and short courses given in connection with major conferences. The approach I advocated is now changing the way the stochastic finite element studies are being carried out—people recognize that the so-called global stiffness matrix cannot be assumed ad hoc, but it has to be related to the micromechanics of the material at hand, according to principles of mechanics.
A related area is the study of impact (e.g. shock) waves in materials and structures, where the interplay of the random micro-heterogeneous structure with the very thin wavefront thickness prevents one from adopting a homogeneous medium assumption. Another field, currently under active development, is the mechanics of fractal materials, Fig. 3.
A development of techniques for study of physically and/or geometrically nonlinear and inelastic structural elements (such as rods, plates, shells, and 3D domains) with material spatial randomness and under random forcing is still awaiting development. This is a major task for the next decades and, once accomplished, the science and engineering communities will have tools for comprehensive studies of full stochastic boundary value problems.
Do you foresee any social or political implications for your research?
The paper leads to a more powerful way of studying multiscale problems in
mechanics of materials with presence of material randomness, especially
those lacking separation of scales, and thus will contribute to further
engineering advances as well as to better understanding and modeling of
biomechanics problems of living systems. One case in point is the mechanics
of traumatic brain injury which I also presently study.![]()
Prof. Martin Ostoja-Starzewski
Department of Mechanical Science and Engineering
also
Member of the Institute for Condensed Matter Theory
and
Part-Time Faculty at Beckman Institute
University of Illinois at Urbana-Champaign
Web
KEYWORDS: HETEROGENEOUS BODIES SMALLER; COMPUTATIONAL HOMOGENIZATION; CONTINUUM THERMODYNAMICS; COMPOSITE-MATERIALS; BOUNDARY-CONDITIONS; CUBIC POLYCRYSTALS; ELASTIC PROPERTIES; MINIMUM SIZES; SIMULATION; MICROMECHANICS.
