Tom Goldstein & Stanley Osher Discuss the Split Bregman Method for L1-Regularized Problems
New Hot Paper Commentary, July 2011

|
Article: The Split Bregman Method for L1-Regularized Problems
Authors: Goldstein, T;Osher,
S |
Tom Goldstein & Stanley Osher talk with ScienceWatch.com and answer a few questions about this month's New Hot Paper in the field of Computer Science.
![]() Why do you think your paper is highly
cited?
Why do you think your paper is highly
cited?
Our paper is highly cited because it gives state-of-the-art fast, simple, and versatile numerical algorithms for solving a class of problems of great practical and theoretical significance. These problems include recovering signals, images, and videos from perhaps very sparse data. The method can also be used to restore signals, images, and video by removing noise, reversing blur, filling in missing data, etc. Application areas range from medical imaging (such as MRI, fMRI, CT, ultrasound) to intelligence (hyperspectral imaging), to commercial (the Net?ix problem), and beyond.
![]() Does it describe a new discovery, methodology, or
synthesis of knowledge?
Does it describe a new discovery, methodology, or
synthesis of knowledge?

Coauthor Stanley Osher
It represents a new discovery in that this class of algorithms is shown to be remarkably effective for many convex optimization problems involving regularizers which are homogeneous of degree one. Problems of this type have taken center stage in fields like compressive sensing, matrix completion, image processing, and more. However the paper is also a synthesis of classical algorithms, such as the augmented Lagrangian method, and the alternating direction method of multipliers.
![]() Would you summarize the significance of your paper
in layman's terms?
Would you summarize the significance of your paper
in layman's terms?
In layman's terms, this is a method which is useful in predicting what movies Net?ix customers might prefer, tracking moving objects in very noisy videos, finding objects on the ground from satellite observations, enabling patients to spend less time in MRI machines, reducing radiation exposure from CT scans, allowing doctors to track needles in ultrasound machines, enabling defense threat reduction by separating aerosols from dust in lidar signals, and more.
![]() How did you become involved in this research, and
how would you describe the particular challenges, setbacks, and
successes that you've encountered along the way?
How did you become involved in this research, and
how would you describe the particular challenges, setbacks, and
successes that you've encountered along the way?
The research developed as part of Tom's Ph.D. thesis and evolved out of earlier work with M. Burger, D. Goldfarb, J.-J. Xu, and W. Yin, using Bregman iteration to improve denoising results. Significant contributions also came with W. Yin, D. Goldfarb, and J. Darbon, who used Bregman iteration to develop a fast algorithm for the L1 based constrained optimization problems arising in compressive sensing.
Figure 1:
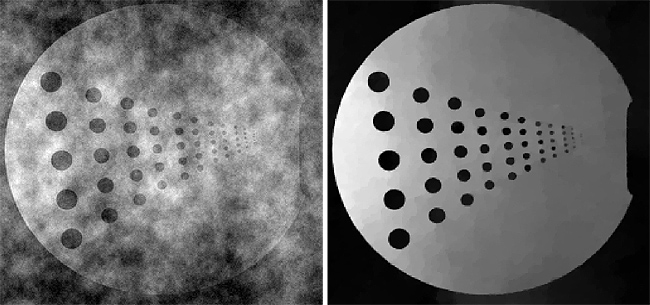
Reconstruction of a Magnetic Resonance (MR) image
using the Split Bregman method for compressed sensing. Only 30% of the
image data was used for reconstruction. (left) The undersampled image is
reconstructed using a conventional method (e.g. fast Fourier transform).
(right) The same data is used to reconstruct a high quality image using the
Split Bregman technique.
New challenges include the search for ways to further speed up the method, and new applications, such as optimizing geometries and imaging through turbulence. Many questions have also arisen about combining Split Bregman with newer algorithms to solve nonlinear problems, such as robust principal component analysis. Success basically comes from seeing this method used in so many areas of science, technology, data mining, statistics, learning theory, and more.
![]() Where do you see your research leading in the
future?
Where do you see your research leading in the
future?
Our research will continue to lead improvements in the applied areas mentioned above. We expect to find new applications and discover new fast methods of interest to various communities. One emerging application is the use of Split Bregman to speed up and improving classical filtering methods for dynamical systems.
![]() Do you foresee any social or political
implications for your research?
Do you foresee any social or political
implications for your research?
Social implications will come from improved medical imaging, marketing (as
in the Net?ix problem), military intelligence (through hyperspectral
imaging, and directing unmanned aerial vehicles, or UAV's), and other
applications for these algorithms.![]()
Tom Goldstein, Ph.D.
Department of Electrical Engineering
Stanford University
Stanford, CA, USA
Professor Stanley Osher
Mathematics, Computer Science and Electrical Engineering departments
and
Institute for Pure and Applied Mathematics
University of California at Los Angeles
Los Angeles, CA, USA
Acknowledgments:
We wish to emphasize that this research was made possible through the generosity of the National Science Foundation, Office of Naval Research and the National Geospatial Intelligence Agency.
KEYWORDS: Bregman, Constrained Optimization, 1 regularization, compressed sensing, total variation denoising.
